全书结构
预备知识
张量
张量表示一个由数值组成的数组,这个数组可能有多个维度。
具有一个轴的张量对应数学上的向量(vector); 具有两个轴的张量对应数学上的矩阵(matrix); 具有两个轴以上的张量没有特殊的数学名称。
张量的创建
import torch
x = torch.arange(12)
x.shape
x.numel()
X = x.reshape(3, 4)
torch.zeros((2, 3, 4))
torch.ones((2, 3, 4))
torch.randn(3, 4)
torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
运算符
按元素运算
常见的运算符这里用作按元素运算。
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x + y, x - y, x * y, x / y, x ** y # **运算符是求幂运算
可以得到
(tensor([ 3., 4., 6., 10.]),
tensor([-1., 0., 2., 6.]),
tensor([ 2., 4., 8., 16.]),
tensor([0.5000, 1.0000, 2.0000, 4.0000]),
tensor([ 1., 4., 16., 64.]))
还有很多的一元运算符都可以用在按元素运算。
线性代数运算
求和/平均值
直接调用sum函数,会将其变成一个标量,也可以指定axis = 1维度来指定轴来进行降维。
A.sum()
A.sum(axis = 1)
A.sum(axis = [0, 1])# 对于矩阵来说,相当于A.sum()
同理,A.mean()也是一样的。
如果希望能够在求和或者平均值的时候保持轴数不变,可以使用keepdims = True。
如果希望能够沿着某个轴计算A元素的累计总和,可以使用cumsum函数。
sum_A = A.sum(axis=1, keepdims=True)
A.cumsum(axis=0)
点积
x = torch.arange(4)
y = torch.ones(4, dtype = torch.float32)
torch.dot(x, y)
矩阵-向量积
当我们为矩阵A和向量x调用torch.mv(A, x)时,会执行矩阵-向量积。 注意,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同。
矩阵-矩阵乘法
我们可以将矩阵-矩阵乘法AB看作简单地执行m次矩阵-向量积,并将结果拼接在一起,形成一个n×m矩阵。
在下面的代码中,我们在A和B上执行矩阵乘法。 这里的A是一个5行4列的矩阵,B是一个4行3列的矩阵。 两者相乘后,我们得到了一个5行3列的矩阵。
B = torch.ones(4, 3)
torch.mm(A, B)
张量连结
在这里,dim=0说明是第一个维度进行拼接;dim=1说明是第二个维度进行拼接。
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
广播机制
特别需要注意这个,可能会导致错误发生。
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a, b
由于a和b分别是3×1和1×2矩阵,如果让它们相加,它们的形状不匹配。 我们将两个矩阵广播为一个更大的3×2矩阵,如下所示:矩阵a将复制列, 矩阵b将复制行,然后再按元素相加。
索引和切片
与Dataframe中相似。
节省内存
如果直接使用X = X + Y就是重新创建一个元素。但是,有些时候希望执行原地操作。
如果希望执行原地操作的话,可以使用两种方式,此时不会占用新的空间:
X[:] = X + Y
X += Y
转换为其他对象
转换为Numpy非常容易:A = X.numpy()
转换为Python标量:a.item()或者使用内置函数float(a)等。
自动求导
自动求导是计算一个函数在指定值上的导数。
- 如何实现?
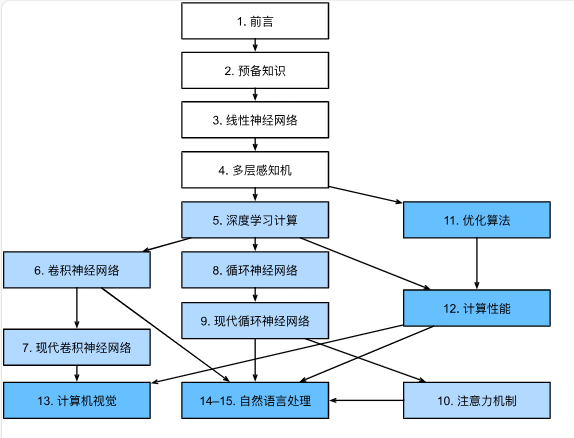
- 计算图:将代码分解成操作子,将计算表示成一个无环图。
关于计算图,有显式构造 vs 隐式构造两种构造方式。
| 特性 | 显式构造 | 隐式构造 |
|---|---|---|
| 计算图构建方式 | 显式定义 | 隐式定义 |
| 计算图类型 | 静态图 | 动态图 |
| 典型框架 | TensorFlow 1.x, Theano | PyTorch, TensorFlow 2.x (Eager) |
有两种求导的方式,对于一个链式法则,我们可以采取正向累积和反向累积(也称反向传递)。
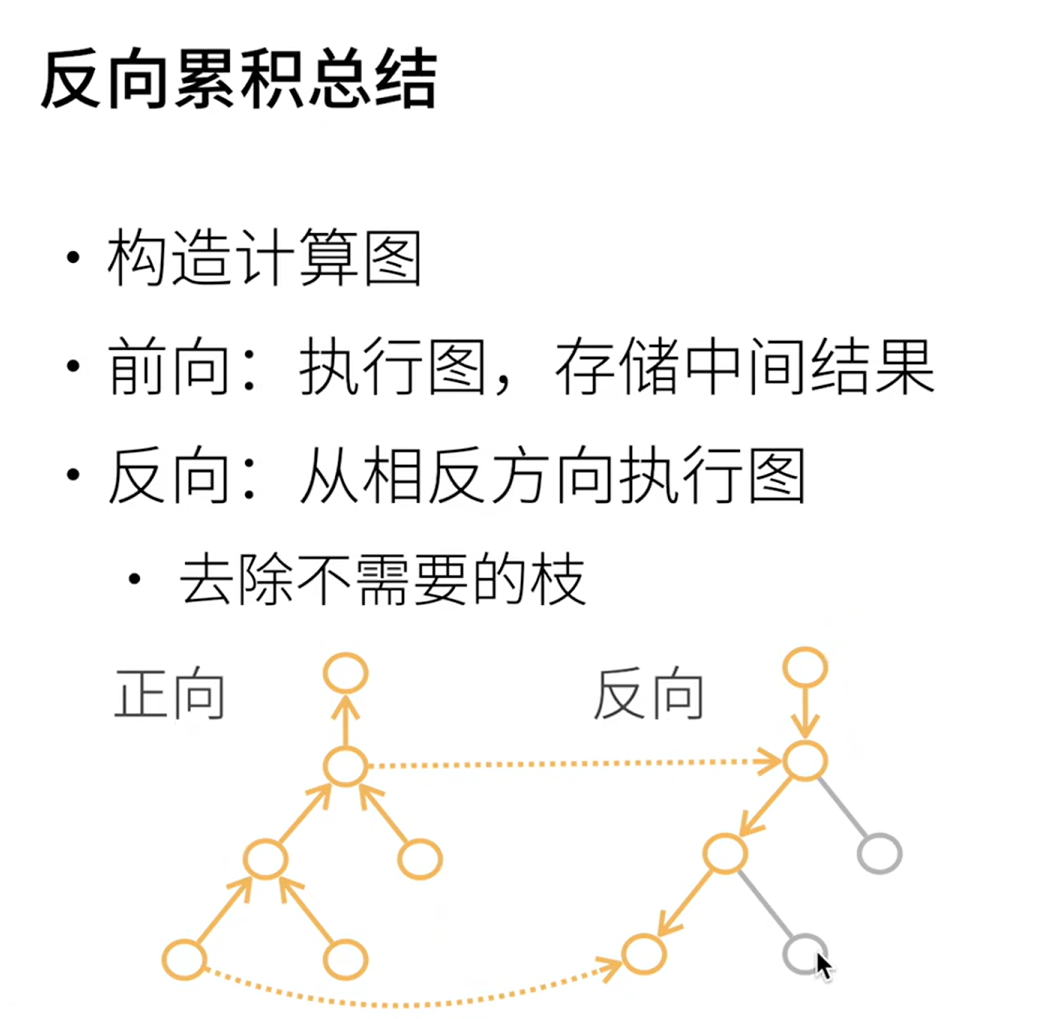
**使用反向传递的时候,在我们计算y关于x的梯度之前,需要一个地方来存储梯度。**重要的是,我们不会在每次对一个参数求导时都分配新的内存。 因为我们经常会成千上万次地更新相同的参数,每次都分配新的内存可能很快就会将内存耗尽。 注意,一个标量函数关于向量x的梯度是向量,并且与x具有相同的形状。
